Thermal Conduction explained in simple terms! Learn the formula, real-life HVAC examples, and tips to reduce heat loss using thermal resistance.
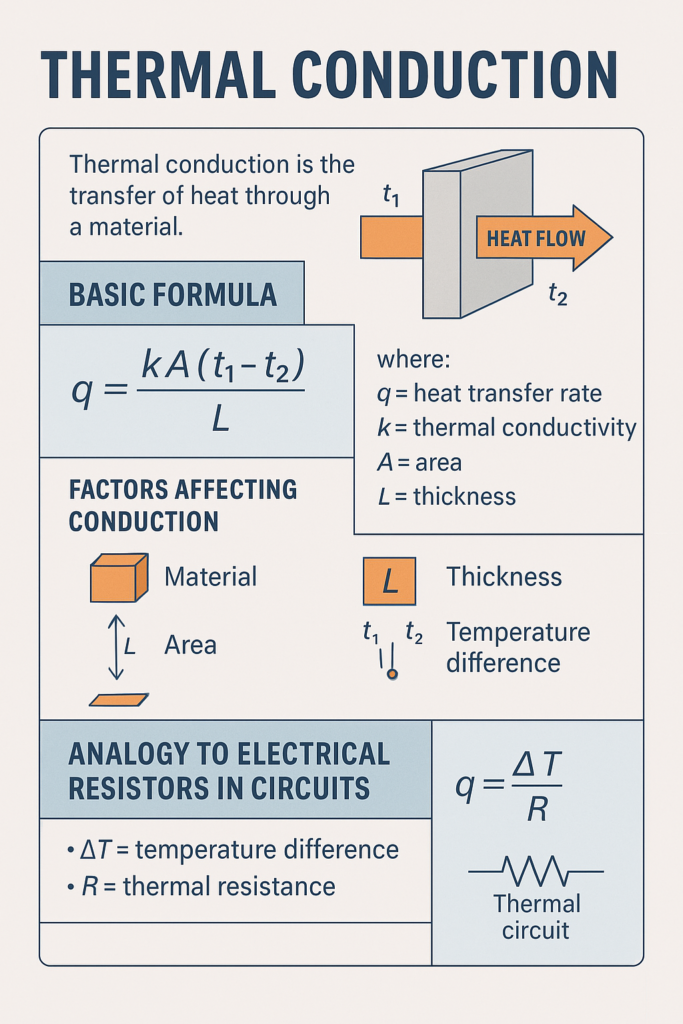

Thermal Conduction explained in simple terms! Learn the formula, real-life HVAC examples, and tips to reduce heat loss using thermal resistance.