Views in the last 30 days: 16
Estimated read time: 5 minute(s)
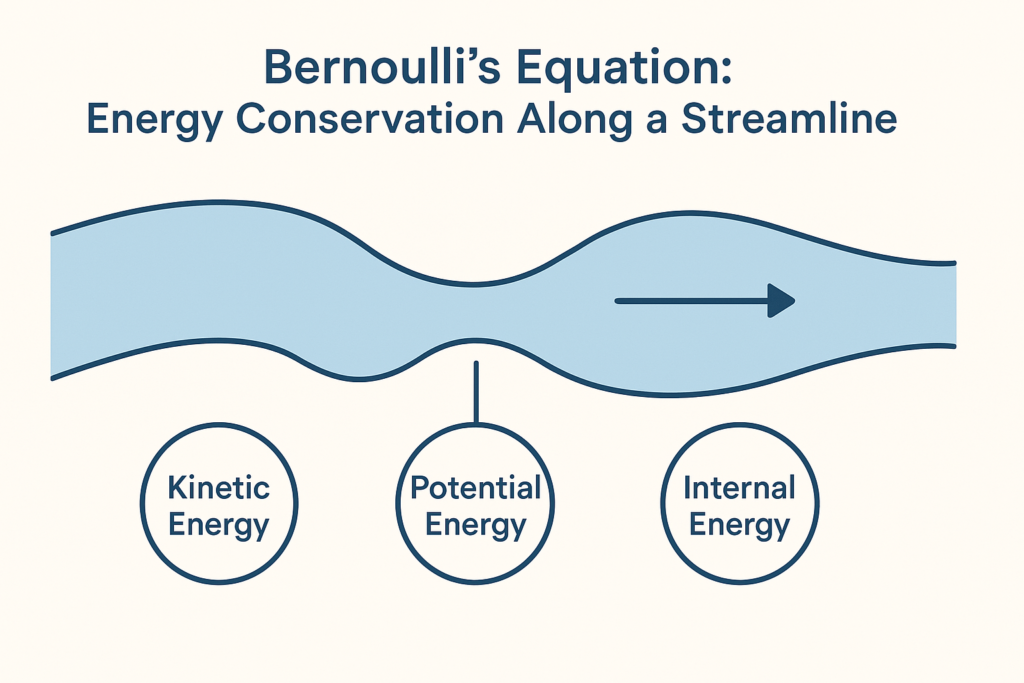
Imagine you’re playing with a toy water slide. When you let water flow down the slide, you might notice that it speeds up in some parts and slows down in others. Bernoulli’s Equation is a bit like a “magic rule” that tells us how the energy of moving water (or any fluid) is shared between its speed, the pressure it’s under, and how high up it is. In simple words, it explains why water sometimes flows faster and its pressure drops, and vice versa!
What Is Bernoulli’s Equation? 🤔
At its heart, Bernoulli’s Equation is based on the conservation of energy. It tells us that as a fluid (like air or water) moves along a smooth path (called a streamline), the sum of three types of energy remains constant if we ignore losses like friction or heat transfer. These three energies are:
Pressure Energy
Think of pressure as the “push” the fluid has. In our equation, pressure energy per unit weight is expressed as:
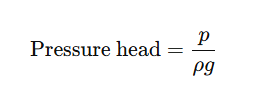
where:
- p is the static pressure (how hard the fluid pushes on its container) in pascals (Pa).
- ρ is the fluid density (how heavy the fluid is per unit volume) in kilograms per cubic meter (kg/m³).
- g is the acceleration due to gravity (about 9.8 m/s²).
Kinetic Energy
This is the energy due to the fluid’s speed. It’s given as:
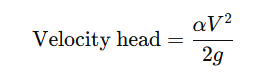
where:
- V is the average velocity of the fluid (m/s).
- α (the kinetic energy correction factor) accounts for the shape of the velocity profile. For an ideal, uniform flow, α is 1; however, if the speed varies across the flow (like in a pipe where the center moves faster than the edges), α can be a bit higher (for example, 1.5 or even 2 in some laminar flows).
Potential Energy
This energy comes from the fluid’s height and is called gravitational potential energy. It’s written as simply:
where:
- z is the elevation (or height) of the fluid above a chosen reference level (in meters).
Elevation head=z
According to Bernoulli’s principle, if we ignore losses, the sum of these three “heads” stays the same along a streamline:
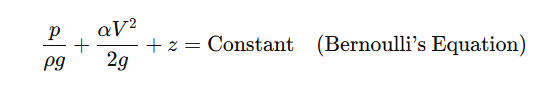
This constant is sometimes called the Bernoulli constant (or total head).
Breaking It Down in Everyday Terms 💡
- Pressure Head (p/ρg)
Imagine you’re holding a water balloon. The pressure inside the balloon tells you how strong the water pushes outward. If you squeeze the balloon (increasing its pressure) and then let it go into a narrow opening, the energy stored as pressure changes the way the water flows. - Velocity Head (αV2/g)
Think of riding a roller coaster. When you start going down, you pick up speed (kinetic energy). In a fluid, if the water speeds up in a narrow section of a pipe, its kinetic energy increases—even though the total energy stays constant. - Elevation Head (z)
Imagine pouring water from a jug. Water held high up has potential energy because gravity is waiting to pull it down. As the water falls, that potential energy is converted to kinetic energy (speed) and sometimes pressure, depending on the pipe’s shape and restrictions.
Important Points to Remember 📌
- Streamline Flow: Bernoulli’s Equation only applies along a streamline—a path followed by particles in steady (unchanging) flow.
- Ideal Conditions: It assumes no friction (viscous losses) and no heat exchange with the surroundings. In real HVAC systems, some losses occur, but this equation is still a great starting point for understanding flow behavior.
- Correction Factor α\alphaα: In most HVAC applications (like air ducts or water pipes), the flow is turbulent and the velocity profile is flatter. This often lets engineers use α≈1, which simplifies calculations.
Welcome to the introduction! In this section, we explain the basics with clear language and detailed examples. You can include
line breaks, bullet lists, and much more.
- Simple explanation
- Easy-to-follow tips
- Engaging content
This is a sample paragraph to show how detailed, paragraph-style text can be formatted.
Bernoulli’s Equation is a principle that balances pressure, velocity, and elevation in a moving fluid. Think of it as the energy statement for flowing fluids, very much like how you balance your allowance between spending and saving.
Key Terms:
- Pressure Head:
p/(ρg)– The energy of fluid pressure. - Velocity Head:
αV²/(2g)– The energy from the fluid’s speed. - Elevation Head:
z– The potential energy from height.
In a perfect system, the sum of these remains constant along a streamline:
p/(ρg) + αV²/(2g) + z = Constant
This section covers how Bernoulli’s Equation applies in real HVAC scenarios. For example, when water flows through a narrowing pipe, the speed increases while the pressure drops—very useful for designing water supply networks and duct systems!
You can add lists, extra paragraphs, bold text, and even images (if needed) directly inside each section.
Bernoulli’s Constant Calculator
This calculator uses the simplified Bernoulli’s Equation (loss‑free) to compute the total constant along a fluid’s streamline:
p/(ρg) + α·V²/(2g) + z = Constant
where:
- p = Static Pressure (Pa)
- ρ = Fluid Density (kg/m³)
- V = Velocity (m/s)
- α = Kinetic Energy Correction Factor (unitless; default is 1)
- z = Elevation (m)
- g = 9.8 m/s² (gravity)
A Simple Real‑World Example 🚰
Let’s say water flows through a horizontal pipe that suddenly narrows. According to Bernoulli’s Equation, when the pipe narrows:
- The water speeds up (increased velocity head).
- The pressure drops (decreased pressure head).
Why? Because the total energy has to remain constant. The gain in kinetic energy (speed) comes from a loss in pressure energy. This is why when you cover part of a garden hose’s opening, the water shoots out faster even though you might feel less pressure at the nozzle.