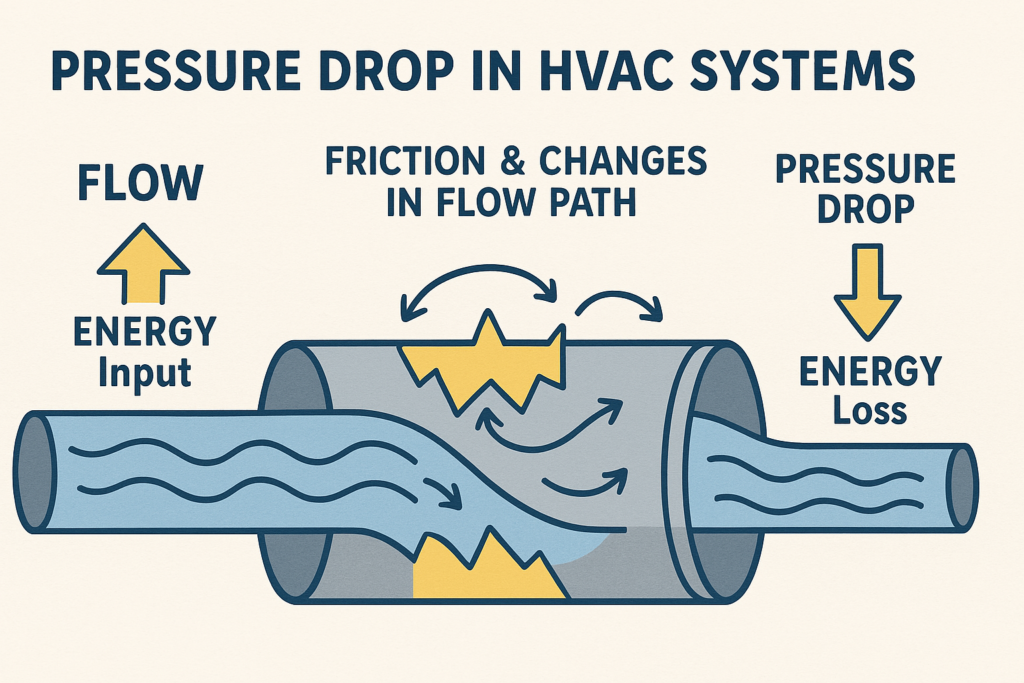
Friction and Fittings

How Flow Loses Energy: Friction and Fittings in Real Systems 🚰💡

/ Calculators, Free, HVAC, NFPA / By

Pressure drop in HVAC systems happens due to friction and flow changes, causing energy loss. Learn how it impacts performance and how to manage it efficiently.

Membership Required

You must be a member to access this content.

View Membership Levels

Already a member? Log in here
Post Views: 83

Related Posts